2022. 10. 1. 21:45ㆍ선형대수
목차
Matrix Operation(행렬 연산)
- equality
- summation
- scalar multiplication
- matrix multiplication
- operation in vector
- geometric interpretation of matrix multiplication
이번에는 행렬의 "기본적인" 연산들에 대해 알아보겠습니다.
참고로, 이번 포스팅에서 다루는 내용 말고도 행렬에 대해서는 훨씬 더 많은 연산이 있지만,
그 연산들은 이후의 포스팅에서 다루도록 하겠습니다.
Matrix Operation(행렬 연산)
- equality(상등)
두 행렬이 상등이라는 의미는 두 행렬이 실제로는 두 개가 아닌 하나라는 즉, 두 행렬이 일치한다는 의미입니다.
예를 들어, 어떤 두 m by n (m \(\times\) n) 행렬 \(A\)와 \(B\)가 아래와 같이 있다고 했을 때,
\(A = \begin{bmatrix}
a_{11} & \cdots & a_{1n} \\
\vdots & \ddots & \vdots \\
a_{m1} & \cdots & a_{mn}
\end{bmatrix} \)
\(B = \begin{bmatrix}
b_{11} & \cdots & b_{1n} \\
\vdots & \ddots & \vdots \\
b_{m1} & \cdots & b_{mn}
\end{bmatrix} \)
\(a_{ij} = b_{ij}\)일 때, 두 행렬 \(A\)와 \(B\)가 상등이라고 말할 수 있습니다.
즉, \(a_{11} = b_{11}\), \(a_{12} = b_{12}\), \(a_{13} = b_{13}\), \(\cdots\) 처럼
두 행렬의 각 자리에 있는 성분(entry)이 모두 동일한 경우에 두 행렬이 상등이라고 할 수 있습니다.
- summation(덧셈)
행렬의 summation(덧셈)은 원소별(element-wise) 연산을 따릅니다.
원소별 연산이란, 각 자리의 원소끼리 연산을 한다는 의미로
동일한 i와 j에 대하여 \(a_{ij}\) + \(b_{ij}\)와 같은 방식으로 연산한다는 것을 의미합니다.
예를 들어, 위의 두 행렬 \(A\)와 \(B\)를 더하면
\(A + B = \begin{bmatrix}
a_{11} + b_{11} & \cdots & a_{1n} + b_{1n} \\
\vdots & \ddots & \vdots \\
a_{m1} + b_{m1} & \cdots & a_{mn} + b_{mn}
\end{bmatrix} \)
와 같은 결과를 얻을 수 있습니다.
- scalar multiplication(스칼라 곱)
행렬의 스칼라 곱이란, 어떤 체(Field)의 원소인 스칼라 \(c\)와 벡터 공간의 원소인 벡터 \(A\)를 곱하여
새로운 벡터 \(c\)\(A\)를 만들어 내는 연산입니다.
(참고로 행렬 집합도 벡터 공간에 해당한다는 것을 이전의 포스팅에서 확인하였습니다)
대부분의 문제에서 우리는 실수 체(Field)만 다룰 것이므로 행렬의 스칼라 곱이란 행렬의 원소에 어떤 실수를 곱하는 것이라고 생각하시면 될 것 같습니다.
예를 들어, 어떤 실수 \(c\) (실수 체의 스칼라 \(c\))와 위의 행렬 \(A\)의 스칼라 곱인 \(c\)\(A\)의 경우는 아래와 같이, 행렬의 모든 원소에 스칼라 c를 곱하면 됩니다.
\(c\)\(A = \begin{bmatrix}
ca_{11} & \cdots & ca_{1n} \\
\vdots & \ddots & \vdots \\
ca_{m1} & \cdots & ca_{mn}
\end{bmatrix} \)
- matrix multiplication(행렬 곱)
행렬 곱은 스칼라와 행렬의 곱인 스칼라 곱과 달리 행렬끼리의 곱셈을 의미합니다.
행렬 곱에 대해서는 결론부터 말하고, 예제와 함께 자세히 설명하도록 하겠습니다.
어떤 행렬 \(C\)와 \(D\)가 있다고 했을 때,
\(C\)가 (m \(\times\) n) 행렬이고, \(D\)가 (n \(\times\) p) 행렬인 경우
\(C\)와 \(D\)의 곱인 \(E = CD\)는 (m \(\times\) p)행렬이 되고
\(E\)의 i번째 행과 j번째 열에 있는 원소인 \(e_{ij}\)는 \(C\)의 i번째 행의 원소들과
\(D\)의 j번째 열의 원소들을 각각 곱해서 더한 값이 됩니다.
행렬 곱에 대해 잘 모르시는 분들은 이게 대체 무슨 말인지 싶을 텐데,
간단한 예제와 함께 어떤 식으로 행렬 곱 연산이 진행되는지 확인해 보겠습니다.
\(C\)와 \(D\)가 각각
\(C = \begin{bmatrix}
c_{11} & c_{12} & c_{13} \\
c_{21} & c_{22} & c_{23}
\end{bmatrix} = \begin{bmatrix}
1 & 5 & 9 \\
4 & 3 & 2
\end{bmatrix}\), \(D = \begin{bmatrix}
d_{11} & d_{12} \\
d_{21} & d_{22} \\
d_{31} & d_{32}
\end{bmatrix} = \begin{bmatrix}
3 & 2 \\
4 & 5 \\
1 & 2
\end{bmatrix}\)
라고 했을 때, \(C\)의 첫번째 행과 \(D\)의 첫번째 열을 원소별로 곱한 후 더한
\(c_{11}d_{11} + c_{12}d_{21} + c_{13}d_{31}\) = 1*3 + 5*4 + 9*1 = 32가
\(E\)의 \(e_{11}\)이 되고,
\(C\)의 첫번째 행과 \(D\)의 두번째 열을 원소별로 곱한 후 더한
\(c_{11}d_{12} + c_{12}d_{22} + c_{13}d_{32}\) = 1*2 + 5*5 + 9*2 = 45가
\(E\)의 \(e_{12}\)가 되고,
\(C\)의 두번째 행과 \(D\)의 첫번째 열을 원소별로 곱한 후 더한
\(c_{21}d_{11} + c_{22}d_{21} + c_{23}d_{31}\) = 4*3 + 3*4 + 2*1 = 26이
\(E\)의 \(e_{21}\)이 되고,
\(C\)의 두번째 행과 \(D\)의 두번째 열을 원소별로 곱한 후 더한
\(c_{21}d_{12} + c_{22}d_{22} + c_{23}d_{32}\) = 4*2 + 3*5 + 2*2 = 27이
\(E\)의 \(e_{22}\)가 되어
\(E = \begin{bmatrix}
e_{11} & e_{12} \\
e_{21} & e_{22}
\end{bmatrix} = \begin{bmatrix}
32 & 45 \\
26 & 27
\end{bmatrix} \)가 됩니다.
행렬 곱에서 유의하셔야 할 점은 (m \(\times\) n) 행렬과 (n \(\times\) p) 행렬의 곱에서
앞 행렬의 열의 수 (m \(\times\) n에서 n)와
뒷 행렬의 행의 수 (n \(\times\) p에서 n)가 같아야 한다는 점입니다.
- operation in vector
이전 포스팅에서 벡터를 행렬의 특수한 형태로 표현하겠다고 하였습니다.
따라서 벡터 또한 행렬의 특수한 형태이니,
모든 열 벡터나 행 벡터에 대해 위에서 다룬
equality, summation, scalar multiplication, matrix multiplication을 적용 가능합니다.
- geometric interpretation of matrix multiplication (행렬 곱의 기하적 해석)
행렬 곱의 기하적인 의미는
바로 차원을 바꾼다는 것입니다.
위의 행렬 곱에서 (m \(\times\) n) 행렬과 (n \(\times\) p) 행렬을 곱하면
(m \(\times\) p)인 행렬이 결과로서 나온다고 언급하였고
열 벡터의 경우에도 matrix multiplication이 성립한다고 언급하였습니다.
그럼 이제, 행렬과 벡터의 matrix multiplication에 대해 생각해 보겠습니다.
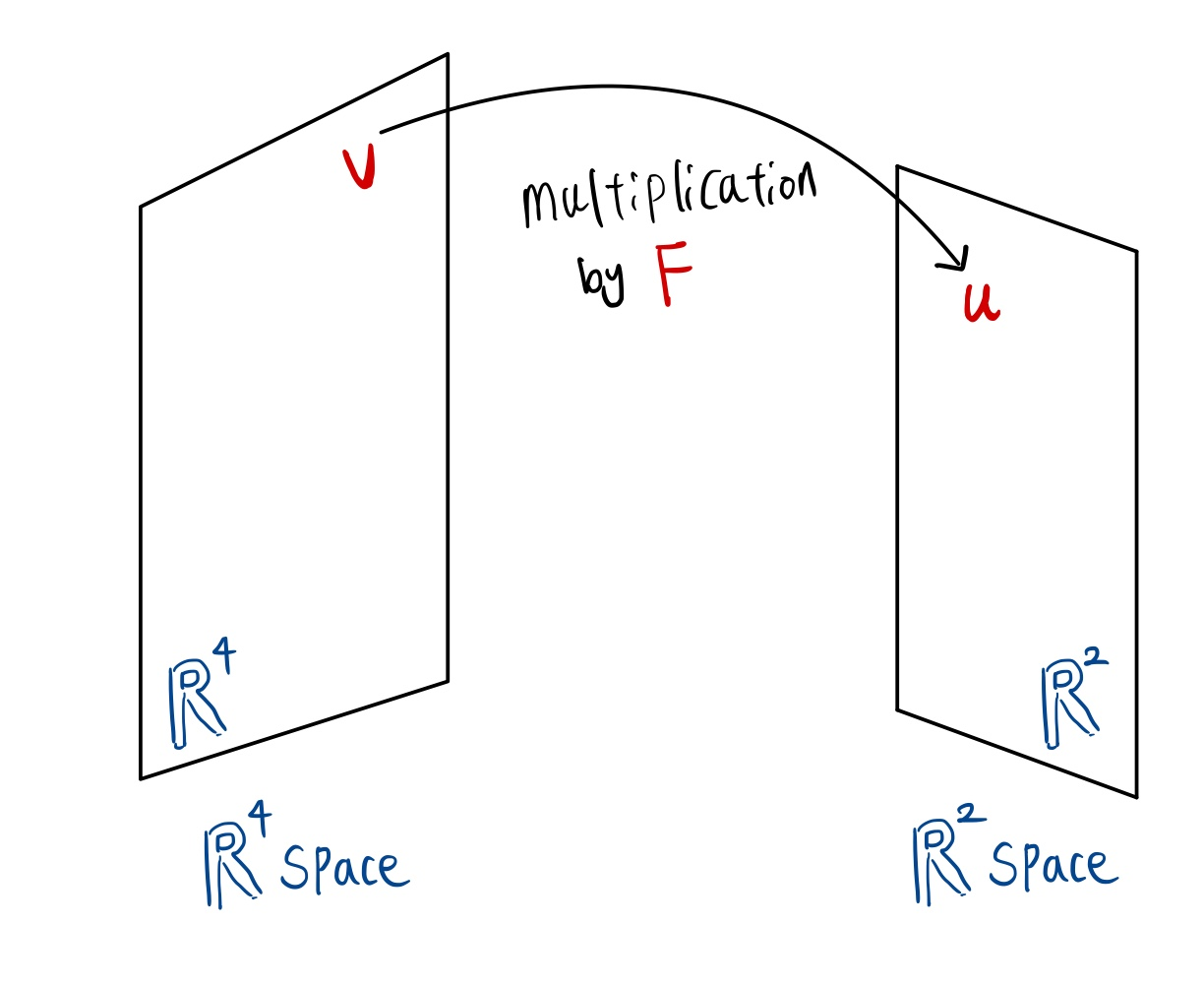
어떤 행렬 \(F\)가 (2 \(\times\) 4) 행렬이고,
\(\mathbb{R}^4\)의 벡터 \(\mathbf{v} = \begin{bmatrix}
v_{1} \\
v_{2} \\
v_{3} \\
v_{4}
\end{bmatrix} \) 가 있다고 했을 때 (4 \(\times\) 1),
행렬 곱 \(\mathbf{u}\) = \(F\)\(\mathbf{v}\)는 (2 \(\times\) 1) 의 형태를 가진 \(\mathbb{R}^2\)의 벡터 \(\mathbf{u} = \begin{bmatrix}
u_{1} \\
u_{2}
\end{bmatrix} \)가 되고,
이는 결과적으로 행렬 곱의 결과 벡터가 변환되어 벡터의 차원이 \(\mathbb{R}^4\)에서 \(\mathbb{R}^2\)으로 이동한 것입니다.
이 포스팅은 'linear algebra and its applications 5th edition'을 보고 공부한 내용을 정리하여 작성하였습니다.

'선형대수' 카테고리의 다른 글
| Vector Equation (벡터 방정식), Matrix Equation (행렬 방정식) (0) | 2022.10.04 |
|---|---|
| Span (생성), Subspace (부분 공간) (0) | 2022.10.02 |
| Vector Space (벡터 공간), Vector (벡터) (2) | 2022.09.30 |
| 군 (Group), 환 (Ring), 체 (Field) (2) | 2022.09.29 |
| Elementary Row Operation (기본 행 연산), Row Reduction (행 줄임), Pivot (0) | 2022.09.27 |