2022. 9. 27. 20:21ㆍ선형대수
목차
Elementary Row Operation (기본 행 연산)
- Elementary Row Operation
- Row Equivalent
Row Reduction (행 줄임)
- Echelon Form (= row echelon form)
- Reduced Echelon Form (= reduced row echelon form)
- Uniqueness of reduced echelon form
- Row reduction
- Pivot
- Partial Pivoting
이전 포스팅에서는 linear system을 matrix로 표기하는 방법인 matrix notaion에 대해 다루면서
matrix에 row reduction을 적용하면 linear system의 solution을 구할 수 있다고 했습니다.
이번 포스팅에서는 이 row reduction이 무엇인지에 대해 알아보도록 하겠습니다.
Elementary Row Operation (기본 행 연산)
- elementary row operation
row reduction을 다루기 전에 우선 elementary row operation과 row equivalent라는 개념에 대해 다루겠습니다.
elementary row operation (기본 행 연산)은 글자 그대로 행렬에서 할 수 있는 operation을 의미합니다.
elementary row operation에는 Interchange, Scailing, Replacement 세 가지가 있습니다.
우선, elementary row operation을 적용할 예제로서 아래와 같은 행렬을 가정하겠습니다.
\begin{bmatrix} a_{1,1} & a_{1,2} & a_{1,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ a_{3,1} & a_{3,2} & a_{3,3} \end{bmatrix}
1. Interchange
Interchange란,
행렬에서 두 행을 통째로 바꾸는 operation을 의미합니다.
예를 들어,
\begin{bmatrix} a_{3,1} & a_{3,2} & a_{3,3} \\ a_{2,1} & a_{2,2} & a_{2,3} \\ a_{1,1} & a_{1,2} & a_{1,3} \end{bmatrix}
와 같은 행렬은 예제 행렬에서 첫 번째 행과 세 번째 행을 바꾸어 Interchange operation을 적용한 행렬입니다.
2. Scailing
Scailing이란,
행렬에서 특정한 행의 모든 성분(entry)에 0이 아닌 상수를 곱하는 operation을 의미합니다.
예를 들어,
\begin{bmatrix}
a_{1,1} & a_{1,2} & a_{1,3} \\
a_{2,1} & a_{2,2} & a_{2,3} \\
ka_{3,1} & ka_{3,2} & ka_{3,3}
\end{bmatrix}
(단, \(k \neq 0\))
와 같은 행렬은 예제 행렬에서 세 번째 행의 모든 entry에 0이 아닌 상수 k를 곱하여 Scailing operation을 적용한 행렬입니다.
3. Replacement
Replacement란,
행렬에서 어떤 하나의 행에, 다른 행에 Scailing operation을 적용한 것을 더하는 operation을 의미합니다.
예를 들어,
\begin{bmatrix}
a_{1,1} + ka_{2,1} & a_{1,2} + ka_{2,2} & a_{1,3} + ka_{2,3} \\
a_{2,1} & a_{2,2} & a_{2,3} \\
a_{3,1} & a_{3,2} & a_{3,3}
\end{bmatrix}
(단, \(k \neq 0\))
와 같은 행렬은 예제 행렬에서 첫 번째 행에, 두 번째 행에 Scailing 한 것을 더하여
Replacement operation을 적용한 행렬입니다.
- row equivalent
어떤 두 행렬이 elementary row operation을 적용하여 만들어지는 관계라면 이 두 행렬을 row equivalent 하다고 합니다.
예를 들어,
\begin{bmatrix}
a_{1,1} & a_{1,2} & a_{1,3} \\
a_{2,1} & a_{2,2} & a_{2,3} \\
a_{3,1} & a_{3,2} & a_{3,3}
\end{bmatrix}
행렬과
\begin{bmatrix}
a_{1,1} + ka_{2,1} & a_{1,2} + ka_{2,2} & a_{1,3} + ka_{2,3} \\
a_{2,1} & a_{2,2} & a_{2,3} \\
a_{3,1} & a_{3,2} & a_{3,3}
\end{bmatrix}
(단, \(k \neq 0\))
행렬은 elementary row operation을 적용한 결과 만들어지므로 row equivalent합니다.
추가로 만약 두 행렬이 row equivalent 하다면 두 행렬로 표시된 linear system들은 같은 solution set을 가진다는 특징이 있습니다.
Row Reduction (행 줄임)
row reduction이라는 것은 행렬을 echelon form(사다리꼴 행렬 형태)이나 reduced echelon form으로 만드는 작업을 뜻합니다.
그러므로 우선은 echelon form과 reduced echelon form을 먼저 설명하도록 하겠습니다.
- echelon form ( = row echelon form)
echelon form은 행렬의 특수한 형태로 아래의 세 가지 조건을 만족하는 행렬을 의미합니다.
조건 1. 모든 nonzero rows는 all zero rows보다 항상 위에 있어야 한다.
여기서 all zero row란, 특정 행의 모든 성분(entry)이 모두 0인 행을 뜻하고
nonzero row란 특정 행의 모든 성분(entry)이 모두 0은 아닌 행 즉, 행의 모든 성분들 중 단 하나라도 0이 아닌 성분이 있는 행을 의미합니다.
예를 들어,
\begin{bmatrix}
2 & 0 & 1 & 4 \\
0 & 0 & 0 & 1 \\
0 & 0 & 0 & 0
\end{bmatrix}
와 같은 행렬에서 첫 번째 행과 두 번째 행은 nonzero row, 세 번째 행은 all zero row에 해당합니다.
all zero row가 아닌 경우를 nonzero row로 보셔도 무방합니다.
조건 2. nonzero rows 사이에서, 아래쪽 행의 leading entry는 위쪽 행의 leading entry보다 오른쪽 열에 있어야 한다.
여기서 leading entry란, 각각의 row에서 첫번째로 나오는 0이 아닌 값을 의미합니다.
예를 들어,
\begin{bmatrix}
2 & 0 & 1 & 4 \\
0 & 0 & 7 & 3 \\
0 & 0 & 0 & 5
\end{bmatrix}
라는 행렬에서, 첫 번째 행의 leading entry는 2가 되고, 두 번째 행의 leading entry는 7이 되며, 세 번째 행의 leading entry는 5가 됩니다.
조건 3. leading entry와 같은 열(column) 내에서 leading entry보다 아래쪽 행에 있는 값은 모두 0이어야 한다.

위의 그림과 같은 상황이 조건 3을 만족하는 상황이라고 볼 수 있습니다.
- reduced echelon form ( = reduced row echelon form)
reduced echelon form이란 echelon form의 보다 더 특수한 형태를 의미합니다.
reduced echelon form은 echelon form의 조건 1, 2, 3을 만족하면서 추가로 아래의 두 가지 조건을 더 만족하는 행렬을 의미합니다.
조건 4. 모든 leading entry의 값은 1이어야 한다.
말 그대로의 의미입니다. leading entry에 해당하는 값이 1이면 됩니다.
조건 5. leading entry와 같은 열(column) 내에서 leading entry를 제외한 값은 모두 0이어야 한다.
조건 3과 비슷하지만 살짝 다릅니다.
조건 3의 경우 leading entry보다 아래에 있는 값들만 0이면 되지만
조건 5의 경우 leading entry가 있는 열이라면 leading entry보다 아래에 있는 값은 물론 위에 있는 값까지 모두 0이 되어야 합니다.
예를 들어 위에 있는 '그림 1'의 경우는 조건 3은 만족하지만 조건 5는 만족하지 못합니다.
(물론 조건 4도 만족하지 못합니다.)
이는 leading entry와 같은 열에 있는 값들 중 leading entry보다 위에 있는 값들이 0이 아니기 때문입니다.
echelon form과 reduced echelon form에 대해 배워보았으니 이제 몇 가지 예시를 보고 행렬들을 구분해 보겠습니다.

예제 1의 경우, 조건 1, 2, 3을 모두 만족하지만 조건 4, 5를 모두 만족하지 않아 echelon form이 됩니다.

예제 2의 경우, 조건 1, 2, 3을 모두 만족하고 조건 4, 5도 모두 만족하기에 reduced echelon form이 됩니다.

예제 3의 경우, 조건 1을 만족하지 않아 echelon form이 되지 못합니다.

예제 4의 경우, 조건 3을 만족하지 않아 echelon form이 되지 못합니다. (조건 2도 만족하지 못합니다.)
- uniqueness of reduced echelon form
reduced echelon form과 관련된 성질이 하나 있습니다.
그것은 각각의 matrix(행렬)가 오직 하나의 reduced echelon form과 row equivalent하다는 것입니다.
즉, 어떤 행렬에 row reduction을 하여 그 행렬을 reduced echelon form으로 만든다고 하였을 때,
얻을 수 있는 reduced echelon form은 단 한 가지라는 뜻이고, 이를 unique하다고 합니다.
좀 더 자세히 설명하자면, 행렬 A에 row reduction을 적용하여 Ar이라는 reduced echelon form을 얻었을때
행렬 A에 row reduction을 다른 순서로 여러번 적용한다 할지라도 결국 항상 Ar과 똑같은 reduced echelon form을 가진다는 이야기입니다.
(행렬 A와 다른 행렬 B가 있다고 한다면 B의 reduced echelon form은 Ar과 다를 수 있습니다.)
- row reduction
row reduction이란, matrix(행렬)에 elementary row operation을 여러번 적용하여 reduced echelon form으로 만드는 일종의 알고리즘에 해당합니다.
예제를 가지고 row reduction을 실행해 보는 편이 더 좋을 것 같아 예제를 가져왔습니다.
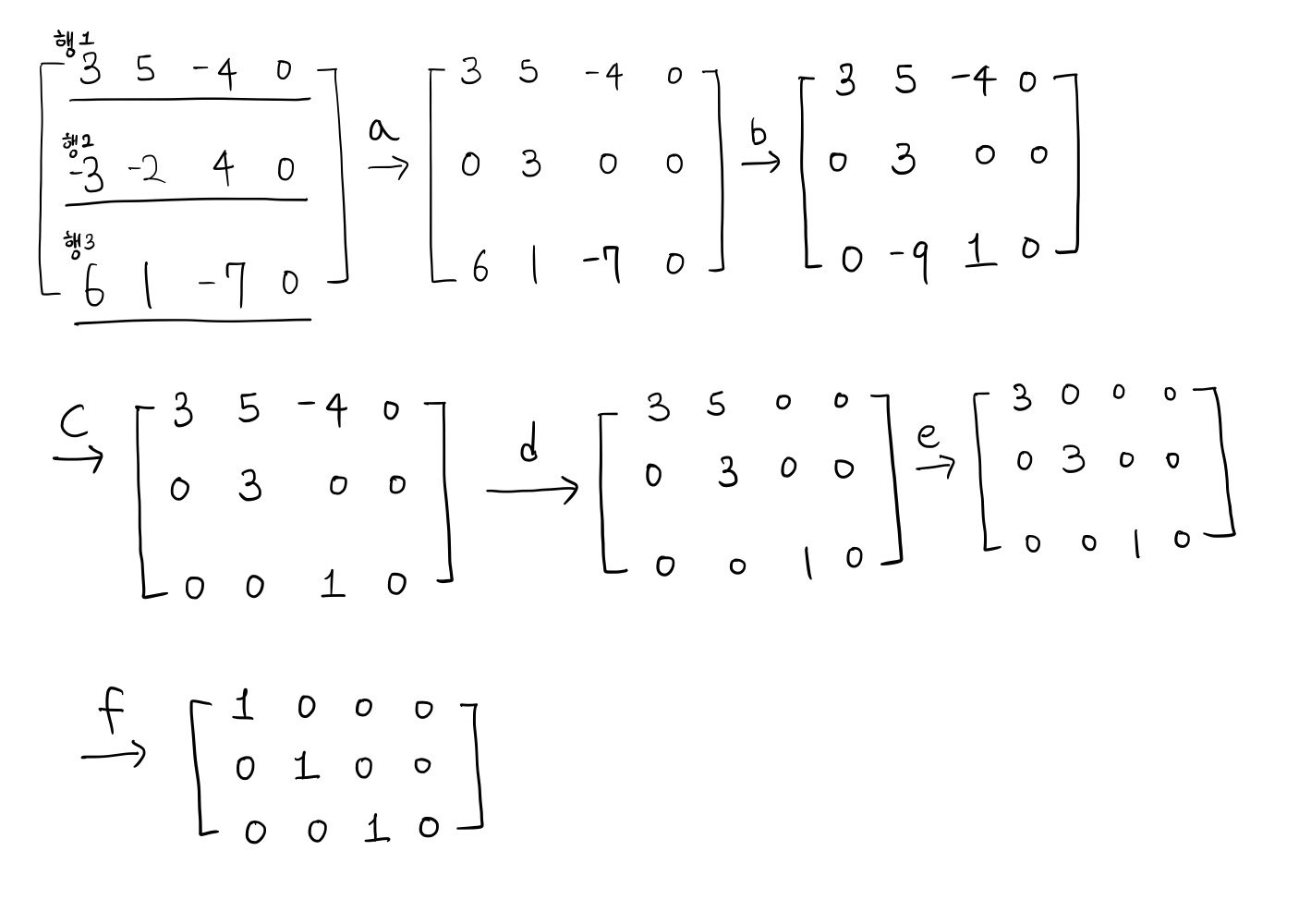
그림에서 우선 제일 위쪽 행의 leading entry와 같은 열에 있고 아래에 있는 값들을 0으로 만들기 위해
a단계에서 행1을 행2에 더해주었고 (Replacement) b단계에서는 행1에 -2를 곱하여 행3에 더해주었습니다(Replacement).
그 이후에는 행2의 leading entry와 같은 열에 있고 아래에 있는 값을 0으로 만들기 위해 c단계에서 행2에 3을 곱하여 행3에 더해주었습니다(Replacement).
그리하여 우선은 echelon form의 형태가 되었고 이제 더 나아가 reduced echelon form을 만들기 위해
leading entry와 같은 열에 있는 모든 값들을 0으로 만들어 주기 위해 d단계에서는 행3에 4를 곱하여 행1에 더해 주었고(Replacement)
e단계에서는 행2에 \(-{5 \over 3}\)를 곱하여 행1에 더해주었습니다(Replacement).
마지막으로 f단계에서는 leading entry를 모두 1로 만들기 위해 행1과 행2에 각각 \({1 \over 3}\)을 곱해주었습니다(Scailing).
예제에서는 쓰이지 않았지만 만약 \(\begin{bmatrix}
0 & 0 & 0 & 0
\end{bmatrix}\)과 같은 행이 행1, 행2 or 행3보다 위에 있었다면 이때는 조건 1을 만족시키기 위해 제일 먼저 row switching으로 \(\begin{bmatrix}
0 & 0 & 0 & 0
\end{bmatrix}\) 같은 행을 아래로 내려주면 됩니다.
- Pivot
Echelon Form과 관련된 용어들 중, Pivot이라는 용어가 존재합니다.
pivot이란, 어떠한 matrix를 echelon form으로 만들었을 때, 각 행의 leading entry에 해당하는 성분을 을 이야기하고, pivot의 위치를 pivot position이라고 하며, pivot이 포함된 column을 pivot column이라고 합니다.
예를 들어,
\(\begin{bmatrix}
1 & -2 & -1 & 3 \\
0 & -3 & -6 & 4 \\
-1 & 5 & 0 & 3
\end{bmatrix}\) 와 같은 matrix가 있을 때, 이의 row echelon form은
\(\begin{bmatrix}
1 & -2 & -1 & 3 \\
0 & -3 & -6 & 4 \\
0 & 0 & -7 & 10
\end{bmatrix}\)가 되므로, pivot column은 1, 2, 3열이 되고, 첫번째 행의 pivot은 1행 1열의 성분인 1이 됩니다.
- Partial Pivoting
Row Reduction에서는 처음에 가장 왼쪽에 있는 nonzero column을 pivot column으로 설정하고, 그 때의 nonzero enrty를 pivot으로 설정한 후, 그 pivot이 있는 row를 가장 위쪽으로 Interchange하는 방식을 주로 이용합니다.
예를 들어, \(\begin{bmatrix}
0 & -3 & -6 & 4 \\
2 & -2 & -1 & 3 \\
-1 & 5 & 0 & 3
\end{bmatrix}\)
와 같은 matrix에 Row reduction을 적용할 때, 가장 왼쪽에 있는 nonzero column인 첫번째 column을 pivot column으로 설정하고, pivot column에 있는 두 값인 2과 -1 중 하나를 pivot으로 정하여 그 pivot이 있는 row를 가장 위에 놓는 식으로 적용합니다. 즉,
\(\begin{bmatrix}
-1 & 5 & 0 & 3 \\
2 & -2 & -1 & 3 \\
0 & -3 & -6 & 4 \\
\end{bmatrix}\) 와 같은 식으로 Row reduction을 적용합니다.
Partial Pivoting이란, 위와 같이 pivot column에서 pivot을 지정하는 과정에서, 절댓값이 큰 값을 우선적으로 pivot으로 정하는 방법을 의미합니다.
위의 \(\begin{bmatrix}
0 & -3 & -6 & 4 \\
2 & -2 & -1 & 3 \\
-1 & 5 & 0 & 3
\end{bmatrix}\) matrix에 Partial Pivoting 방법을 적용하면
\(\begin{bmatrix}
2 & -2 & -1 & 3 \\
0 & -3 & -6 & 4 \\
-1 & 5 & 0 & 3
\end{bmatrix}\) 와 같은 방식으로 Row reduction을 적용하게 됩니다.
이 포스팅은 'linear algebra and its applications 5th edition'을 보고 공부한 내용을 정리하여 작성하였습니다.

'선형대수' 카테고리의 다른 글
| Matrix Operation 1 (행렬 연산) (0) | 2022.10.01 |
|---|---|
| Vector Space (벡터 공간), Vector (벡터) (2) | 2022.09.30 |
| 군 (Group), 환 (Ring), 체 (Field) (2) | 2022.09.29 |
| Matrix Notation (행렬 표기법) (2) | 2022.09.26 |
| Linear Equation(선형 방정식), Linear System(선형 계) (0) | 2022.09.25 |