Probability Terminology (확률 용어)

목차

 

Probability

• Experiment
• Sample Space
• Probability Value
• Equally likely

 

Events

• Event
• Elementary Event
• Complement
• Intersection
• Mutually Exclusive
• Difference
• Union
• Partition

 

---

Probability (확률)

 

 

- Experiment (실험)

결과(Outcome)가 정해져 있지 않고 확률적으로 결정되는 실행을 Experiment라고 합니다.

 

ex) 동전 던지기, 주사위 던지기

- Sample Space (표본 공간)

실험의 결과(outcome)로 나올 수 있는 모든 가능한 경우를 원소로 가지는 집합을 Sample Space라고 합니다.

 

ex) 1~ 6까지의 눈을 가지는 두 주사위 dice1, dice2가 있고, outcome을 주사위를 던져서 나온 (dice1의 값, dice2의 값)이라고 할 때, 이 때의 Sample Space를 \(S\) 라고 하면,

\(S = \left \{(1, 1), (1, 2), \cdots , (2, 1), \cdots, (6, 5), (6, 6) \right\}\)

 

- Probability Value (확률 값)

Sample Space \(S = \left \{O_1, O_2, \cdots, O_n \right\}\)의 확률 값이 각각 \(p_1, p_2, \cdots, p_n\) 이라고 했을 때,

\(P(O_i) = p_i\)로 표기할 수 있으며 각각의  \(p_i (i = 1,2, \cdots, n)\)들은 아래의 두 조건을 만족해야 합니다.

\(0 \le p_i \le 1\) and \(\sum_{i=1}^n p_i\)

(각각의 확률 값은 0 이상 1이하, 확률 값의 총합은 1)

 

 

- Equally likely 

Sample space의 outcomes의 probability value가 같은 경우, 이를 equally likely 하다고 합니다.

 

ex) 어떤 sample space가 \(n\)개의 outcomes로 구성되어 있고 모든 outcomes가 equally likely할 경우, 각각의 outcome의 probability value는 \(1/n\) 

(참고로, 모든 outcomes의 확률 값이 같은 경우만 equally likely라고 하는 것은 아닙니다. 2개의 outcomes의 확률 값만 같은 경우에는 두 outcomes가 equally likely 하다고 합니다.)

 

 

 

 

 

 

 

Events (사건들)

 

 

- Event (사건)

Sample Space의 어떤 부분 집합을 Event라고 합니다.

어떤 Event \(A\)에 대해, \(A\)의 확률인 \(P(A)\)는 Event \(A\)에 속한 모든 outcomes의 probability values의 합에 해당합니다.

ex) 1~6까지의 눈을 가지고, 각 눈의 확률이 같은 주사위가 있을 때, 주사위 눈을 던져 짝수가 나오는 경우를 Event \(A\)라고 하면

여기에서의 Sample Space는 \(S = \left \{1, 2, 3, 4, 5, 6 \right\}\),
Event는 \(A = \left \{2, 4, 6 \right\}\), Event \(A\)가 일어날 확률 \(P(A)\) 는 \(P(A) =  P(2) + P(4) + P(6) = 1/6 + 1/6 + 1/6 = 3/6 = 1/2 = 0.5\)

 

- Elementary Event (근원 사건)

Sample Space의 부분 집합들 중 오직 하나의 Outcome으로만 구성된 부분 집합을 Elementary Event라고 합니다.

 

ex) 1~ 6까지의 눈을 가지는 주사위를 던지는 시행에 대해, Outcome을 주사위를 던져서 나온 값이라고 하면

이때의 Sample Space는 \(S = \left \{1, 2, 3, 4, 5, 6 \right\}\)이고,

근원 사건들은 \(\left \{1 \right\} , \left \{2 \right\}, \left \{3 \right\}, \left \{4 \right\}, \left \{5 \right\}, \left \{6 \right\}\)

 

- Complement (여사건)

어떤 Event \(A\)의 Complement를 \(A^\prime\)라고 하며, \(A^\prime\)은 Sample Space에 속하면서 동시에 \(A\)에 속하지 않는 모든 outcomes로 구성된 Event를 의미합니다.

그리고  \(A\)와 \(A^\prime\)에 대해, \(P(A) + P(A^\prime) = 1\) 이 항상 성립합니다.

- Intersection (교집합)

어떤 두 Events \(A\), \(B\)의 intersection을 \(A \cap B\)라고 하며, \(A \cap B\)는  \(A\), \(B\)에 모두 속하는 outcomes로 구성된 Event 입니다.

\(A \cap B\)의 확률을 \(P(A \cap B)\)라고 하며 \(P(A \cap B)\)는 \(A \cap B\)에 속하는 모든 outcomes 의 probability values의 합에 해당하고, \(A\)와 \(B\)가 동시에 일어날 확률이라고도 해석 가능합니다.

ex) 1~ 6까지의 눈을 가지는 주사위를 던지는 시행에 대해, outcome을 주사위를 던져서 나온 값이라고 하고 모든 outcomes가 equally likely 하며 주사위를 던진 결과 짝수 값이 나오는 경우를 Event \(A\),  4 이상의 값이 나오는 경우를 Event \(B\)라고 할 때,

\(A = \left \{2, 4, 6 \right\}\),   \(B = \left \{4, 5, 6 \right\}\),   \(A \cap B = \left \{4, 6 \right\}\),   \(P(A \cap B) = P(2) + P(4) = 1/6 + 1/6 = 1/3\)

 

- Mutually Exclusive (상호 배타적)

어떤 두 Events \(A\), \(B\)에 대해 \(A \cap B = \emptyset\)이면 \(A\)와 \(B\)가 Mutually exclusive 하다고 합니다.

 

- Difference (차집합)

어떤 두 Events \(A\), \(B\)의 Difference를 \(A - B\) 혹은 \(B - A\)라고 하며, \(A - B\)는  \(A\)에는 속하지만  \(B\)에는 속하지 않는 outcomes로 구성된 Event 입니다. \(A - B\)를 \(A \cap B^\prime\)과 같이 교집합을 이용해 표현할 수 있습니다.

\(A - B\)의 확률을 \(P(A \cap B^\prime)\) 라고 하며 \(P(A \cap B^\prime)\) 는 \(A \cap B^\prime\)에 속하는 모든 outcomes 의 probability values의 합에 해당합니다.

또, Event \(A\)의 확률 \(P(A)\)에 대해 \(P(A) = P(A \cap B) + P(A \cap B^\prime)\)라는 식이 항상 성립하며,

위의 식에서 \(P(A \cap B^\prime) = P(A) - P(A \cap B)\)라는 사실 또한 알 수 있습니다.

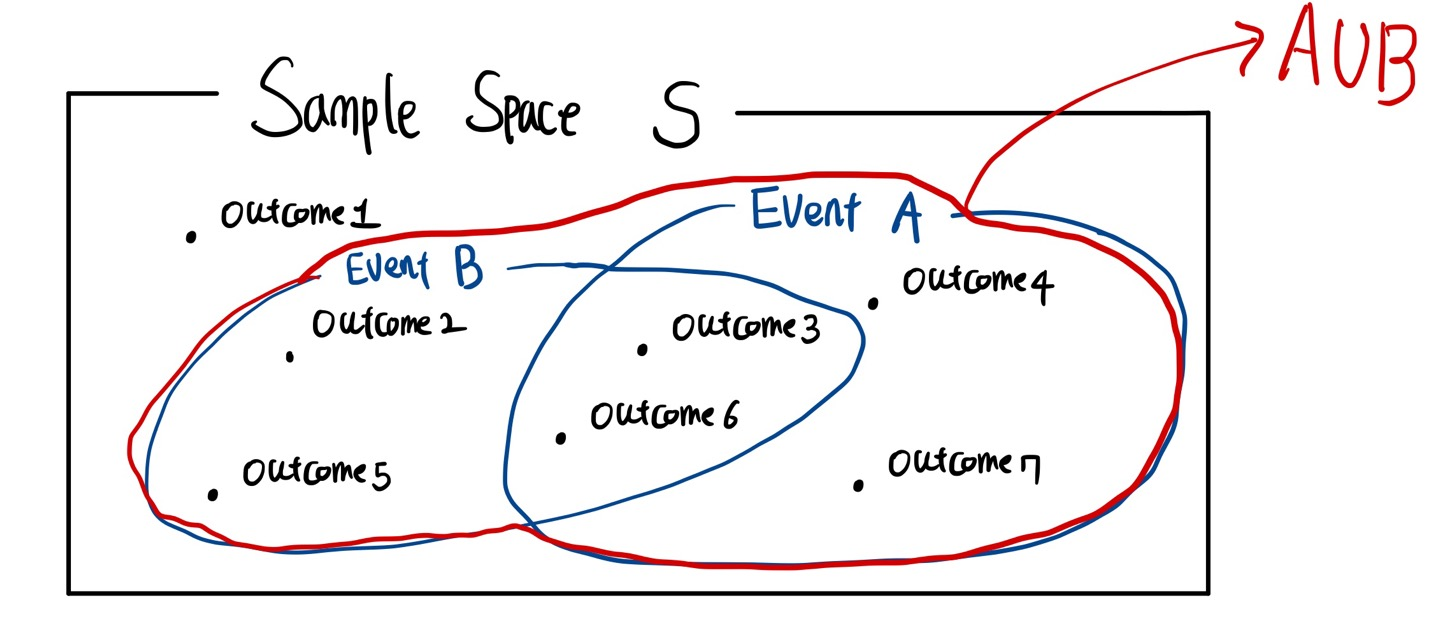
- Union (합집합)

어떤 두 Events \(A\), \(B\)의 Union을 \(A \cup B\)라고 하며, \(A \cup B\)는  \(A\), \(B\) 중 적어도 하나에 속하는 outcomes로 구성된 Event 입니다.

\(A \cup B\)의 확률을 \(P(A \cup B)\)라고 하며 \(P(A \cup B)\)는 \(A \cup B\)에 속하는 모든 outcomes 의 probability values의 합에 해당하고, \(A\)와 \(B\) 중 적어도 하나가 일어날 확률이라고도 해석 가능합니다.

또한 \(P(A \cup B)\)에 대해, \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)라는 식이 항상 성립하며,

\(A, B\)가 Mutually exclusive한 경우 \(A \cap B = \emptyset \)이므로 \(A \cap B\)에 속하는 outcome이 존재하지 않아

\(P(A \cap B) = 0\)이 되어 \(P(A \cup B) = P(A) + P(B)\)이 됩니다.

 

(참고로,  세 Events \(A, B, C\)에 대해서는 \(P(A \cup B \cup C) = P(A) + P(B) + P(C) - P(A \cap B) - P(B \cap C) - P(A \cap C) + P(A \cap B \cap C)\)라는 식이 성립합니다.)

ex) 1~ 6까지의 눈을 가지는 주사위를 던지는 시행에 대해, outcome을 주사위를 던져서 나온 값이라고 하고 모든 outcomes가 equally likely 하며 주사위를 던진 결과 짝수 값이 나오는 경우를 Event \(A\),  4 이상의 값이 나오는 경우를 Event \(B\)라고 할 때,

\(A = \left \{2, 4, 6 \right\}\),   \(B = \left \{4, 5, 6 \right\}\),   \(A \cup B = \left \{2, 4, 5, 6 \right\}\),   \(P(A \cup B) = P(2) + P(4) + P(5) + P(6) = 1/6 + 1/6 + 1/6 + 1/6 = 2/3\)

 

- Partition (분할)

어떤 Sample Space \(S\)의 Events \(A_1, A_2, \cdots , A_n\)들이 모두 공집합이 아니고, Mutually exclusive하며, \(A_1 \cup A_2 \cup \cdots \cup A_n\ = S\)인 경우 \(A_1, A_2, \cdots , A_n\)를 \(S\)의 Partition이라고 합니다.